One Config Change, 22 Models, Wildly Different Results: How KV Cache Precision Reshapes Semantic Drift in Qwen3

In Part 1 we demonstrated that model choice alone can determine whether a 30-step paraphrase chain preserves semantic fidelity or collapses into gibberish. We treated the serving layer as a neutral pipe. That assumption was incorrect.

Ollama’s KV cache defaults to fp16 but supports q8_0 quantization, halving memory footprint at the cost of precision. Re-running the identical 30-iteration telephone-game experiment across the full Qwen3 family (0.6B–80B, multiple weight quantizations) under both KV settings produced dramatic, model-specific shifts: +0.62 for the smallest model, –0.36 for the largest agent-optimized variant. Seventeen of 22 models improved under fp16 KV (mean Δ +0.09). The variance reveals that KV cache precision is not infrastructure trivia—it is a first-class modulator of semantic drift in iterated LLM pipelines.

Recent literature on cultural attractors (Perez et al., 2025), iterative distortion (Mohamed et al., 2025), agent drift (Rath, 2026), and quantization-induced deductive failure (Han et al., 2026) now supplies the mechanistic explanation for these results. This post integrates those findings with our empirical ablation.

Background: KV Cache Precision and Compounding Error in Multi-Hop Chains

Transformers cache key (K) and value (V) projections to enable O(n) attention during autoregressive decoding. fp16 preserves training precision; q8_0 applies uniform 8-bit quantization, introducing per-token rounding noise.

For isolated generations the difference is negligible. In telephone-game chains—where each output becomes the next input—the noise compounds. Mohamed et al. (2025) formalize this as the “broken telephone” effect: factuality (FActScore) and semantic relevance (BERTScore) degrade monotonically across 100 iterations, accelerating with chain complexity. Perez et al. (2025) show that texts converge to cultural attractors—stable fixed points independent of starting content—whose strength and location depend on model size, task constraints, and instruction phrasing. Small models exhibit stronger, more erratic attraction to low-quality basins (e.g., repetitive or gibberish outputs).

Han et al. (2026) prove the Sequential Amortization Failure Theorem: in multi-hop reasoning, quantization noise (weights or activations/KV) violates linear scaling. Early errors become false premises that cascade irreversibly—“deductive drift.” They further show that low-bit KV exacerbates attention-distribution shifts (echoed in KVQuant (Hooper et al., 2024), KIVI (Liu et al., 2024), and KVLinC (2025)), with keys being particularly sensitive due to higher norms and singular values. Our 30-hop paraphrase chain is precisely the regime where these mechanisms surface.

Rath (2026) frames the entire setup as minimal multi-agent interaction and introduces the Agent Stability Index (ASI) to quantify semantic, coordination, and behavioral drift. KV precision directly modulates ASI by altering the stochasticity of attention anchoring.

In short: q8_0 KV injects per-step noise that small models cannot correct (collapse to gibberish attractors) while occasionally regularizing large models away from harmful meta-attractors. fp16 KV removes that noise, amplifying both good and bad basin dynamics. Single-turn benchmarks miss this entirely.

Methodology

Identical to Part 1, single controlled variable:

• Seed prompt: “Step 1: Boil water. Step 2: Add pasta for 8 minutes. Step 3: Drain and serve with sauce.”
• Iteration: “Paraphrase this message for the next agent: [previous]”
• Temperature: 0.7
• Length: 30 iterations
• Metric: Cosine similarity to original via Qwen3-Embedding-0.6B
• KV cache: q8_0 vs. fp16 (Ollama default)
• 22 Qwen3 variants spanning size, weight quant (fp16/q8_0/q4_K_M), and tuning (base/instruct/thinking/next).

Every model ran once per KV setting on identical hardware. All weights were used exactly as provided in the Ollama libraries—no custom post-quantization training or recovery fine-tuning was applied.

Results

Hero plot (seven representative models; solid = fp16 KV, dashed = q8_0 KV):

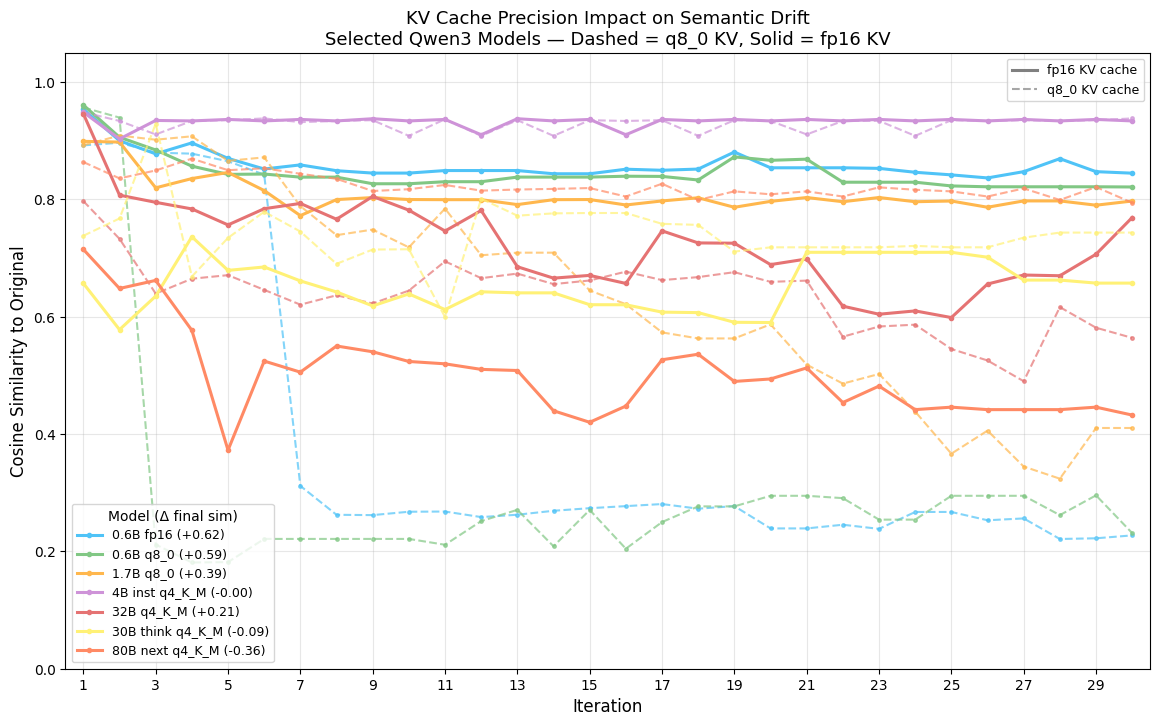
• 0.6B fp16 weights: q8_0 KV → 0.23 (collapse); fp16 KV → 0.84 (+0.62 resurrection).
• 0.6B q8_0 weights: +0.59.
• 1.7B q8_0 weights: +0.39 (crosses usability threshold).
• 4B instruct q4_K_M: flat ~0.93–0.94 (immune).
• 32B q4_K_M: +0.21.
• 30B thinking q4_K_M: –0.09.
• 80B next q4_K_M: 0.79 → 0.43 (–0.36 collapse).

Per-size tables and full interaction heatmap confirm three patterns:

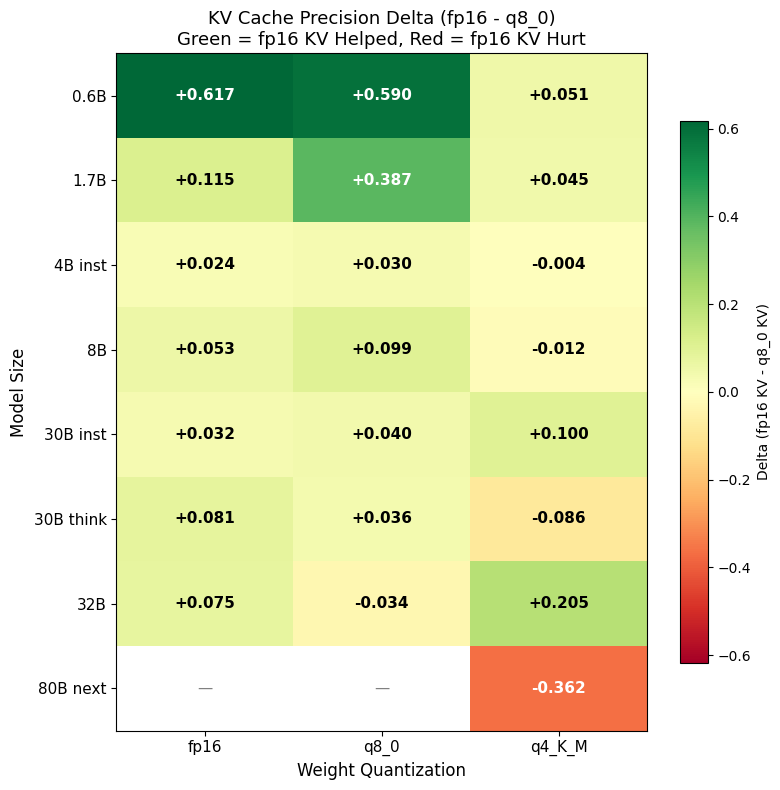
1. Small models (0.6B–1.7B): q8_0 KV noise overwhelms limited capacity → deductive drift (Han et al.). fp16 KV rescues them dramatically, aligning with Perez et al.’s observation that smaller models are more attractor-sensitive.
2. q4_K_M weights: largely immune except for instructive outliers. Weight noise dominates; KV precision becomes second-order (consistent with KVQuant findings on error masking in ultra-low-bit regimes).
3. Non-monotonicity: higher precision is not universally better. Thinking-tuned and agent-optimized variants can regress because fp16 KV strengthens undesirable attractors.

The sorted delta view across all 22 models makes the distribution stark:

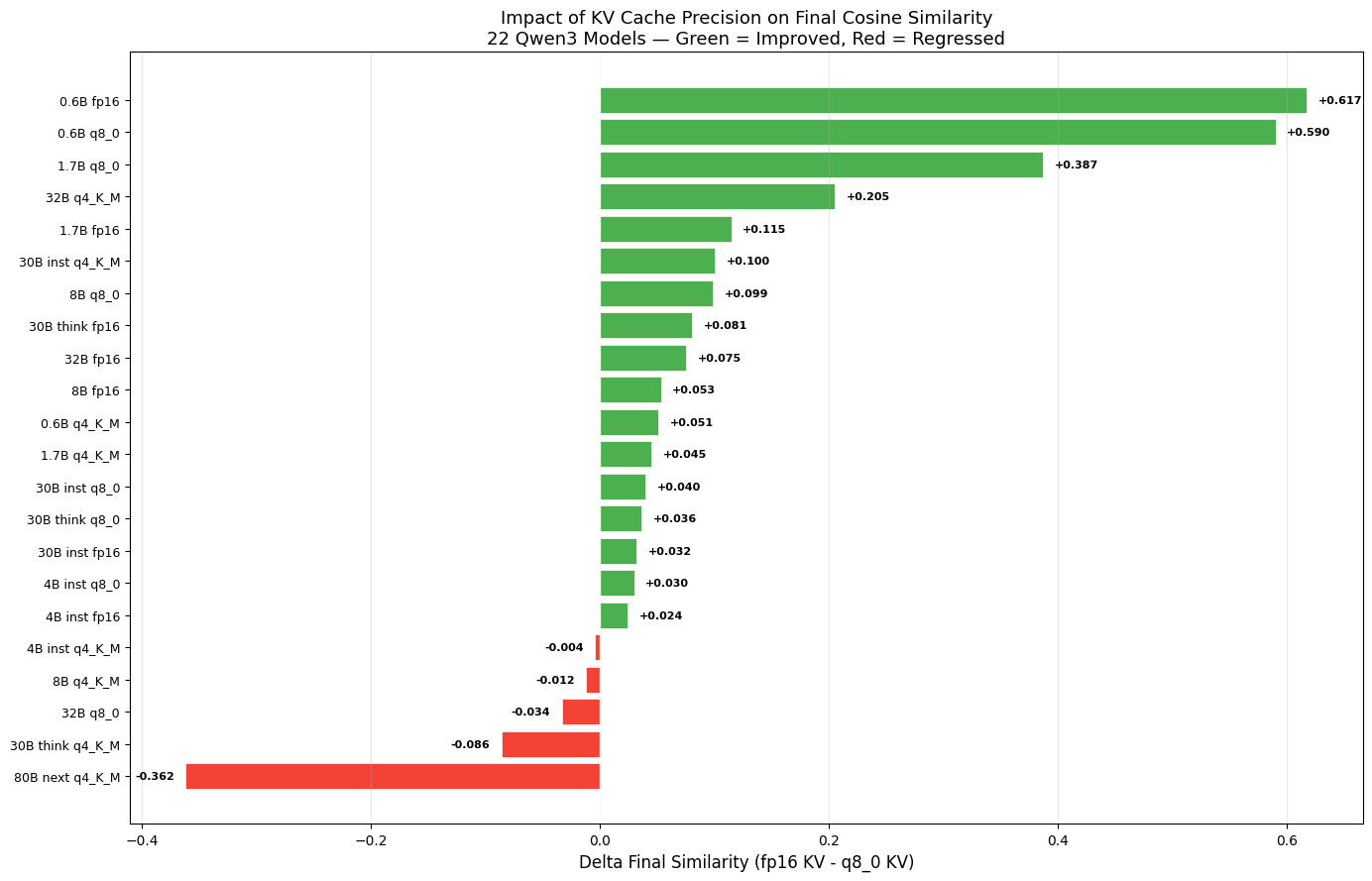
80B qwen3-next anomaly: Under q8_0 KV the model reaches 0.79 (slow drift). Under fp16 KV it collapses to 0.43 by locking into its trained “agent-ready paraphrase” meta-framing attractor earlier and more strongly. As Perez et al. predict, less-constrained or role-specialized models exhibit stronger attractors; Han et al.’s theorem explains why removing quantization noise accelerates convergence to them. Here, q8_0 noise acted as beneficial stochastic regularization—exactly the kind of “helpful noise” Rath (2026) discusses in agent-drift mitigation.

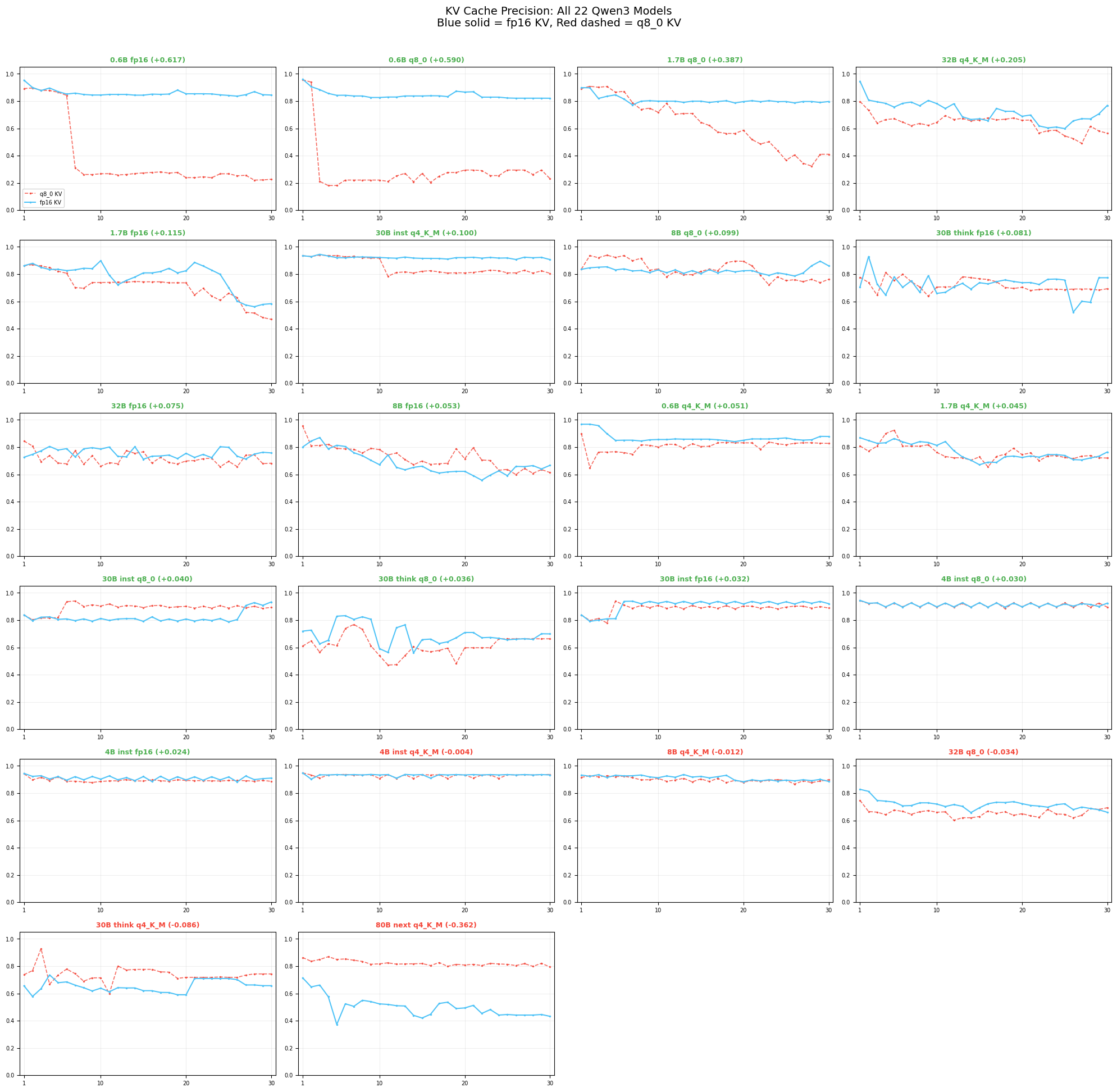
For completeness, every model side by side (blue solid = fp16 KV, red dashed = q8_0 KV):

Insights from the Literature

Our ablation provides the first direct empirical test of KV-precision effects inside a controlled telephone-game setup. It validates and extends:

• Perez et al. (2025): Attractor estimation from early generations matches our 30-hop trajectories. Small-model collapse and large-model meta-drift are textbook examples.
• Mohamed et al. (2025): Distortion is inevitable in iterative generation; our fp16 KV improvements show that reducing per-hop noise is an effective mitigation.
• Han et al. (2026): The Sequential Amortization Failure Theorem directly predicts the +0.62 rescue for capacity-limited models and the non-linear regressions elsewhere.
• Rath (2026): Our chains are minimal multi-agent systems; KV precision modulates the semantic-drift component of ASI.
• Supporting KV-cache work (KVQuant, KIVI, KVLinC, etc.): Explains why keys are more sensitive and why uniform q8_0 produces exactly the attention-distribution shifts we observe in small-model failure modes.

No prior study had ablated serving-config KV precision inside a multi-hop drift benchmark—our results close that gap.

Practical Implications for Agentic Pipelines

1. KV cache is a model-selection hyperparameter. Test at full pipeline depth.
2. Small models need fp16 KV—the difference is existential.
3. q4_K_M offers robustness across serving configs.
4. Agent-optimized models may prefer controlled noise; test before “upgrading” precision.
5. Instruct tuning remains king for drift resistance.
6. Infrastructure changes require re-validation. A single boolean can swing semantic fidelity by 62 points.

Limitations and Unexplored Variables

This study used a fixed experimental setup to isolate KV cache precision as the single variable. Several important factors were held constant and not ablated.

Post-Quantization Training (PQT): All models were used exactly as provided in the Ollama libraries (standard post-training quantization / PTQ GGUF files). We did not examine or control for quantization-aware training (QAT), recovery fine-tuning, or advanced PQT techniques such as GPTQ, AWQ, SmoothQuant, or any custom post-quantization adaptation.

Speculation: Literature consistently shows that QAT or dedicated post-quantization recovery training allows models to adapt to low-precision representations, dramatically reducing error propagation in both weights and activations (D2Quant 2026, EfficientQAT 2025, PTQTP 2025, and multiple surveys on PTQ vs. QAT). Stock Ollama PTQ models may therefore exhibit exaggerated sensitivity to KV cache precision. We suspect that QAT-tuned variants of the same Qwen3 architectures would show much smaller deltas—potentially muting the dramatic +0.62 rescue for tiny models and the –0.36 regression for the 80B agent-tuned variant—because the weights themselves would already be robust to the kind of rounding noise that compounds in chains. This interaction between weight-preparation pipeline and serving-time KV precision is a high-leverage area for future work.

Prompt Engineering: We used one simple structured recipe as the seed prompt and a minimal “Paraphrase this message for the next agent” instruction with no additional system prompt. We did not experiment with system-prompt variations or changes to the paraphrase template.

Speculation: Strong system prompts that explicitly constrain behavior (e.g., “Maintain exact semantic meaning. Preserve all steps verbatim. Never add meta-commentary, agent framing, or explanatory fluff.”) would likely reduce overall drift and shrink the observed KV-precision effect—especially the 80B meta-framing collapse under fp16 KV. Perez et al. (2025) demonstrate that more open-ended instructions produce stronger cultural attractors, while constrained tasks weaken them. Conversely, more creative, open-ended, or complex seed prompts would probably amplify drift and widen the fp16 vs. q8_0 gap, particularly for capacity-limited models. The current procedural prompt was deliberately simple; richer prompting strategies could either mask or exacerbate KV sensitivity.

These limitations mean our results represent one point in a high-dimensional space of serving configuration x model preparation x prompting strategy. The fact that we still saw up to +/-0.62 deltas under these conservative conditions suggests the KV cache effect is quite robust.

Conclusion

Serving-layer KV cache precision is not neutral infrastructure—it is a powerful lever on semantic drift whose effects are predicted by the emerging literature on attractors, broken-telephone distortion, and quantization traps. For most Qwen3 variants fp16 KV improves stability; for capacity-constrained or specially-tuned models the interaction can rescue or ruin performance.

Treat your inference server configuration as part of model selection. Measure drift explicitly at pipeline depth. The difference between 0.23 and 0.84—or 0.79 and 0.43—was literally one config flag.

The telephone game never ends. Precision (and the preparation and prompting that surround it) determines who stays coherent.

References

• Perez, J. et al. (2025). When LLMs Play the Telephone Game: Cultural Attractors as Conceptual Tools to Evaluate LLMs in Multi-turn Settings. ICLR 2025. arXiv:2407.04503.
• Mohamed, A. et al. (2025). LLM as a Broken Telephone: Iterative Generation Distorts Information. ACL 2025. arXiv:2502.20258.
• Rath, A. (2026). Agent Drift: Quantifying Behavioral Degradation in Multi-Agent LLM Systems Over Extended Interactions. arXiv:2601.04170.
• Han, H. et al. (2026). The Quantization Trap: Breaking Linear Scaling Laws in Multi-Hop Reasoning. arXiv:2602.13595.
• Hooper, C. et al. (2024). KVQuant: Towards 10 Million Context Length LLM Inference with KV Cache Quantization. NeurIPS 2024.
• Liu, Z. et al. (2024). KIVI: A Tuning-Free Asymmetric 2-Bit Quantization for KV Cache. ICML 2024.
• Additional KV-cache quantization literature (KVLinC 2025, D2Quant 2026, PTQTP 2025, etc.) as cited inline.
• Part 1: The Telephone Game for Local LLMs: Quantifying Semantic Drift Across 17 Open-Weight Models